1. Interface

以下是最小优先队列所需实现的方法。在这个数据结构中，我们只关心其最小值。

/** (Min) Priority Queue: Allowing tracking and removal of 
  * the smallest item in a priority queue. */
public interface MinPQ<Item> {
    /** Adds the item to the priority queue. */
    public void add(Item x);
    /** Returns the smallest item in the priority queue. */
    public Item getSmallest();
    /** Removes the smallest item from the priority queue. */
    public Item removeSmallest();
    /** Returns the size of the priority queue. */
    public int size();
}

2. MinPQ

我们使用二叉树来实现这个数据结构，但是，它还需要满足以下两个性质：

  1. 每个节点都小于或等于它的两个子节点

  2. 只允许树的最底部有空缺，其他层必须是完整的，且所有节点尽可能靠左

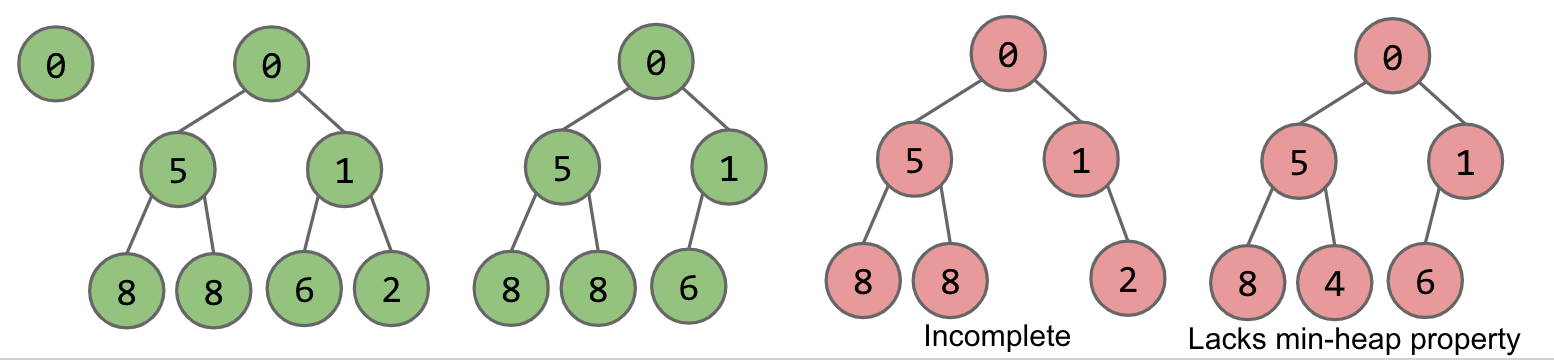
MinPQ.png

在上图中，绿色表示有效的堆，红色则不是

我们同样使用数组来表示这样一棵树。但与 BST 不同，根节点存储在 pq[1] 中，而不是 pq[0]；对于树上的节点 K，它的子节点，父节点位于:

leftChild(k) = 2 * k
rightChild(k) = 2 * k + 1
parent(k) = k / 2

比如根节点（k = 1) 的左节点存储在 pq[2]，右节点存储在 pq[3]，其左右节点的父节点（也就是根节点自身）存储在 pq[1]（2 / 2 = 3 / 2 = 1）

3. Implements

这里是一个 MinPQ的实现

课程 lab10 内容就是实现一个自己的最小堆，这里是我的实现

就像最开始我们实现的链表一样，堆同样会需要resize()操作来调整大小

add

将新 add 的元素添加到队伍末尾，然后调用swim()使其向上“游”到合适的位置

swim()则是不断比较根节点大小，若根节点更大，则交换两者，直到 swim 的元素到比根节点大

public void insert(Key x) {
    // double size of array if necessary
    if (n == pq.length - 1) resize(2 * pq.length);
    
    // add x, and percolate it up to maintain heap invariant
    pq[++n] = x;
    swim(n);
    assert isMinHeap();
}

private void swim(int k) {
    while (k > 1 && greater(k/2, k)) {
        exch(k/2, k);     // swap
        k = k/2;
    }
}

getSmallest

只要返回根节点 pq[1] 便可

removeSmallest

将根节点与数组最末尾的元素进行交换，这样 pq[1] 存放着原先最末尾的元素，然后将 pq 最某位设成 null 删除原来的 root

接着调用sink(1)，使现在的最顶部元素下沉到合适位置

sink()则是不断比较子节点大小，若子节点更小则交换，直到比任何子节点都要小

public Key removeSmallest() {
    if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
    Key min = pq[1];
    exch(1, n--);   // n 表示堆中元素数量
    sink(1);
    pq[n+1] = null;     // to avoid loitering and help with garbage collection
    if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
    assert isMinHeap();
    return min;
}

private void sink(int k) {
    while (2*k <= n) {
        int j = 2*k;
        if (j < n && greater(j, j+1)) j++;
        if (!greater(k, j)) break;
        exch(k, j);
        k = j;
    }
}